6 Mar 2017: Lab 2: Calculating Acceleration due to Gravity

Lab 2:

Calculating Acceleration due to Gravity

Joel Cook

Nina Song

Angel Sanabvia

Lab performed March 2, 2017

In this experiment, we are calculating acceleration due to gravity (g) by using a free fall apparatus and Microsoft Excel.

Introduction: In this lab, we have an apparatus that creates a tape marked every 1/60th of a second. By measuring the distance between the marks on the tape and the time between marks, we are able to calculate acceleration due to gravity. Microsoft Excel, a computer spreadsheet program, is used to perform the calculations and graph the results. In addition, Excel was used to calculate the uncertainty in the data.

Part 1: Calculating g

Procedure: The apparatus pictured below was used to generate the tape with the marks for measuring. The apparatus has a magnet at the top holding a wooden cylinder with a metal ring around the cylinder. A long tape is secured to the apparatus. The cylinder is dropped between two wires and a spark is generated every 1/60th of a second. The metal ring of the cylinder transmits the spark to the tape as it falls making a mark every time the spark is generated. 

The tape was attached to the lab table and the distance between the marks were measured and recorded. A picture of the tape is shown below.

The data was recorded on a spreadsheet to facilitate quickly calculating the mid-interval times and speeds. A graph of the data was generated for mid-interval time vs. speed. A linear fit of the points shows the slope of the line drawn between the points and the slope represents the acceleration. In this case, the acceleration is due to gravity.

After all lab groups were finished calculating acceleration due to gravity, the data was collected on another spreadsheet to analyze the class data for average g calculated, deviation, and the root-mean-square. 

Data and Graphs: The image below shows the data gathered by our lab group.

The columns are labeled to show what the numbers below represent. Formulas were used to quickly calculate the information. TIME is 1/60th of a second for each interval, DISTANCE was measured on the tape in cm, ΔX is the difference between consecutive distances, MID-INTERVAL TIME is each time + 1/120th of a second for the middle of the interval, and MID-INTERVAL SPEED is the ΔDISTANCE/ΔTIME for each interval. A graph was generated from the data calculated that shows the mid-interval speed vs. time.

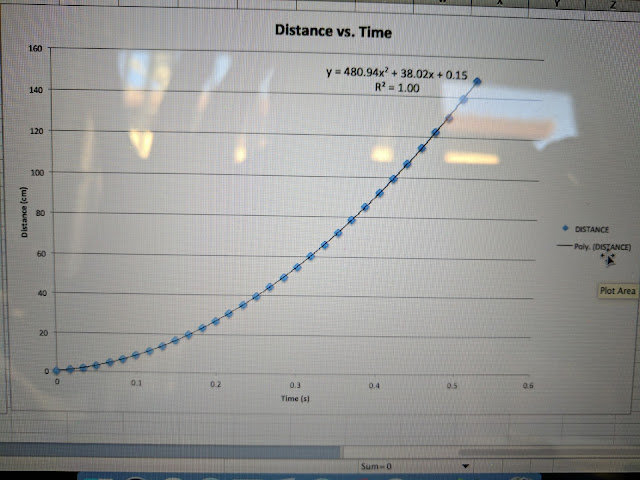
A graph of distance vs. time was created from the data gathered and shown below.

Questions: 

1. For the data presented the value of the mid-interval speed is equal to the average velocity over the same time interval:

Average velocity = ΔX/ΔT = (1.9 - 0.9)/(3/60 - 2/60) = 60 cm/s

Mid-interval speed = ΔX/1/60 = (1.9 - 0.9)/(1/60) = 60 cm/s

2. A linear fit of the data shows a slope of 963.58. This slope of a graph of speed vs. time is the acceleration, in this case acceleration due to gravity in cm/s^2. The calculated g for our group was 9.63 m/s^2. The accepted value for g is 9.8 m/s^2. The value calculated of 9.63 m/s^2 is lower than the accepted value of 9.8 m/s^2 by 0.17 m/s^2.

3. A power fit of the second graph shows a value of 480.94 as the first coefficient. The derivative of distance vs. time gives the equation for speed vs. time with the slope of this line being acceleration. The derivative of this equation gives a linear equation with a value of approximately 962 or 9.62 m/s^2 for acceleration due to gravity. The value calculated of 9.62 m/s^2 is lower than the accepted value of 9.8 m/s^2 by 0.18 m/s^2.

Part 2: Errors and Uncertainty

For the second part of this lab we gathered the class data for acceleration due to gravity and developed the following table:

We calculated the average for g as 962.852 cm/s^2. Next we calculated the root-mean-square to get a standard deviation of 10.0. The class, as a whole, calculated g to be 9.62 +/- 0.10 m/s^2 with 68% certainty (1 standard deviation) and 9.62 +/- 0.20 m/s^2 with 95% certainty (2 standard deviations). since the accepted value for g is 9.8 m/s^2, the class average was consistently below that value but the average value is within 2 standard deviations of the accepted value.

Questions:

1. The pattern in our values of g were that most of the values were less than the accepted value of g.

2. Our group also calculated g at below the accepted value, but within two standard deviations of the accepted value of 9.8 m/s^2.

3.  The pattern for calculated values of g was that most of the groups calculated g at less than the accepted value.

4. Our value of g was very close to the class average. A systematic error that may exist in this experiment are the possibility that the cylinder contacted the wires or tape of the apparatus causing friction and affecting acceleration. A random error that could exist would be the possibility of measuring some of the marks inaccurately with the meter stick. 

5. The objective of this portion of the lab is to explore uncertainty in our experiments and outcomes and discuss calculating the numeric value of this uncertainty to better understand our results. Understanding uncertainty helps to identify the accuracy of the experiment and the results and to identify portions of the experiment or tools that could be improved to increase the accuracy of the outcomes. The key ideas were calculating the average of a set of data, calculating the standard deviation through the root-mean-square method, and explaining errors that may exist in the experiment.

Conclusion: In summation, although our calculation for the acceleration due to gravity for this lab was close to the class average, it was not very close to the actual value of g. Although our value was below the accepted value of g, the importance of the experiment was not in confirming the value of g, but rather in exploring tools to analyze results and determine the accuracy of data sets.