Lab 9: Centripetal Force with a Motor
Joel Cook
Nina Song
Lab performed April 3, 2017

Joel Cook
Nina Song
Lab performed April 3, 2017
The goal of the experiment performed is to model the relationship between the angle, Θ, and angular speed, ω, for a rotating system with a suspended mass.
Introduction: As a suspended mass is rotated about a central access, the angle of formed between the point of suspension and the string suspending the object is related to the speed at which the system rotates. The faster the system rotates about it's axis or rotation, the further the suspended mass swings from the system and the larger the angle, Θ, that is formed. By measuring the height of the object as it rotates, we can calculate the angle and the angular speed of the system. This value can be confirmed by calculating the angular acceleration by measuring the time for the system to complete a rotation.
Apparatus/Procedure:
The above photo shows the apparatus used in the experiment. It consists of a surveying stand with a motor attached. The motor is supplied with a variable voltage to control the speed of rotation. A rod is attached perpendicular to the shaft of the motor and a mass is hung from a string at the end of the rod. The system was allowed to come up to speed and the time for 10 rotations was measured to determine the time for one rotation.
The above photo shows the apparatus used to measure the height of rotation. The ring stand has an arm attached with a piece of paper secured to it. As the mass swung around, the arm was raised until the point at which the mass barely comes into contact with the top of the paper. The height of the top of the paper at that point is recorded. This procedure was repeated at various speeds to develop a set of data points.
The diagram above shows the values that were measured. The height of the apparatus was measured (H), as well as the length of the rod, from motor shaft to point where string is attached, (R), and the length of the string (L).
The values measured were used to determine the Θ and ω.
Data:
|
Time (seconds) for one rotation
|
h (centimeters)
|
|
3.29
|
38.5
|
|
2.79
|
62.3
|
|
2.28
|
93.5
|
|
1.90
|
116.0
|
|
1.60
|
133.4
|
|
1.39
|
142.2
|
The above chart shows the time for one rotation and the heigh, h, at which the mass contacted the top of the paper attached to the ring stand. The time for one rotation was determined by measuring the time for 10 rotations and dividing by 10 to get the time for one rotation. As the speed of rotation increased (time for one rotation decreased), the height of the mass increased.
|
t(s)
|
h(m)
|
(H-h)/L
|
arcos
(H-h)/L
|
Θ
(degrees)
|
ω (from
h)
|
ω (from
t)
|
Δ
|
|
3.29
|
0.385
|
0.886435331
|
0.48121041
|
27.57134881
|
1.857159868
|
1.909781155
|
-0.052621287
|
|
2.79
|
0.623
|
0.736277603
|
0.743243534
|
42.5847536
|
2.223031361
|
2.252035842
|
-0.029004482
|
|
2.28
|
0.935
|
0.539432177
|
1.001033714
|
57.35505543
|
2.70891335
|
2.755780702
|
-0.046867351
|
|
1.9
|
1.16
|
0.397476341
|
1.16203137
|
66.57954938
|
3.203614804
|
3.306936842
|
-0.103322038
|
|
1.6
|
1.334
|
0.287697161
|
1.278974858
|
73.27992338
|
3.792664546
|
3.9269875
|
-0.134322954
|
|
1.39
|
1.422
|
0.232176656
|
1.336481432
|
76.57481014
|
4.232623276
|
4.520273381
|
-0.287650105
|
The chart above shows the data that was calculated from the measured values. The following calculations were used to determine the values above.
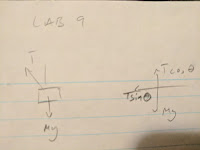
Free Body Diagram for Hanging Mass Net Force Equations
The above calculation shows how we calculated ω from calculating the angle, Θ. The length, r, in the equation was substituted, using trigonometry, with known values. Once Θ was calculated for each angular speed, we could calculate ω.
In the data chart, time (t) was measured, height (h) was measured, and r was calculated from (H-h)/L where H is the height of the apparatus and L is the length of the string. The arccosine of r gives us the angle Θ and by plugging the value for Θ into the equation above we can calculate ω, as shown.
Two different values for ω were calculated in this experiment. The chart shows ω (from h), which is the method just discussed, while ω (from t) was the angular speed determined from converting the time for one rotation to radians/second.
The above graph shows the result of plotting the data on an axis and calculating a proportional fit of the data. The slope of the line should, theoretically, be 1.0 as the values for ω from t and h should be the same.
Conclusion:
As the previous graph shows, the slope of the line through the data generated was 1.0403. This value suggests that the values we calculated for ω from both methods were very close. As the chart below shows, the difference between the two methods was consistently less than 0.28 radians per second and less than 0.13 radians per second if you remove the fastest speed of rotation from the data. Removing the fastest trial from the experiment is prudent as the error in our measured values was higher as the apparatus rotated more quickly. This is because as the apparatus rotates faster, the hanging mass lags further behind the end of the rod due to air resistance. This means the value of LsinΘ is smaller than we are assuming and the effect is worse at higher rotational speeds. In addition, the rod experiences centrifugal force, as it rotates, due to the hanging mass which tends to pull the rod down and lower the height at which the object strikes the paper. This causes our value for h to be lower than it actually is and the effect is worse at higher speeds. Finally, the exact height at which the mass strikes the paper is impossible to determine in our experiment. It is possible that the paper was raised too much between rotations and the value for h was higher than it should have been.
|
ω (from
h)
|
ω (from
t)
|
Δ
|
|
1.857159868
|
1.909781155
|
-0.052621287
|
|
2.223031361
|
2.252035842
|
-0.029004482
|
|
2.70891335
|
2.755780702
|
-0.046867351
|
|
3.203614804
|
3.306936842
|
-0.103322038
|
|
3.792664546
|
3.9269875
|
-0.134322954
|
|
4.232623276
|
4.520273381
|
-0.287650105
|
In conclusion, even though error exists in our measurements, means of measurement, and experimentation, our values calculated for both methods were sufficiently accurate and comparable. The lab was successful and the outcome of the experiment was as predicted.



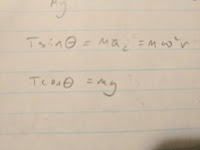


No comments:
Post a Comment